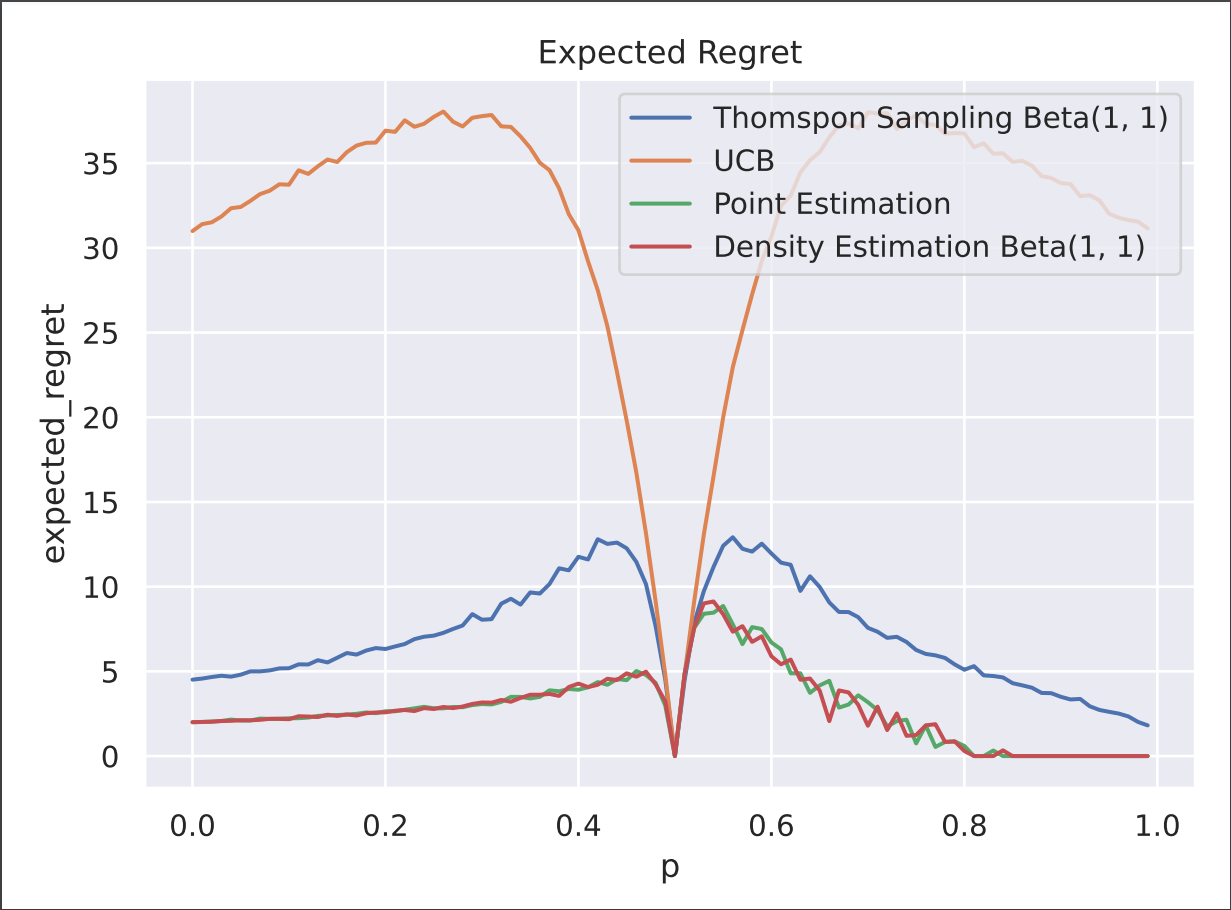
In this experiment, we compare the expected regret of the Bayesian Optimal Policy to popular asymptotically optimal bandit algorithms UCB and Thompson Sampling in the one-armed bandit setting. All algorithm descriptions and equations are shown in the supplementary section. In this case, the stochastic arm has a reward bernoulli distributed with some p ∈ [0, 1] and the deterministic arm has a constant reward of 0.5. We set the priors for the density estimation variant of Bayesian Optimal Policy as well as Thompson Sampling to be beta distributed with α = 1 and β = 1. We plotted the expected regret for all values of p from [0, 1] for all algorithms below in figure 1. We observe both variants of the Bayesian Optimal Policy outperform Thompson Sampling and UCB. 

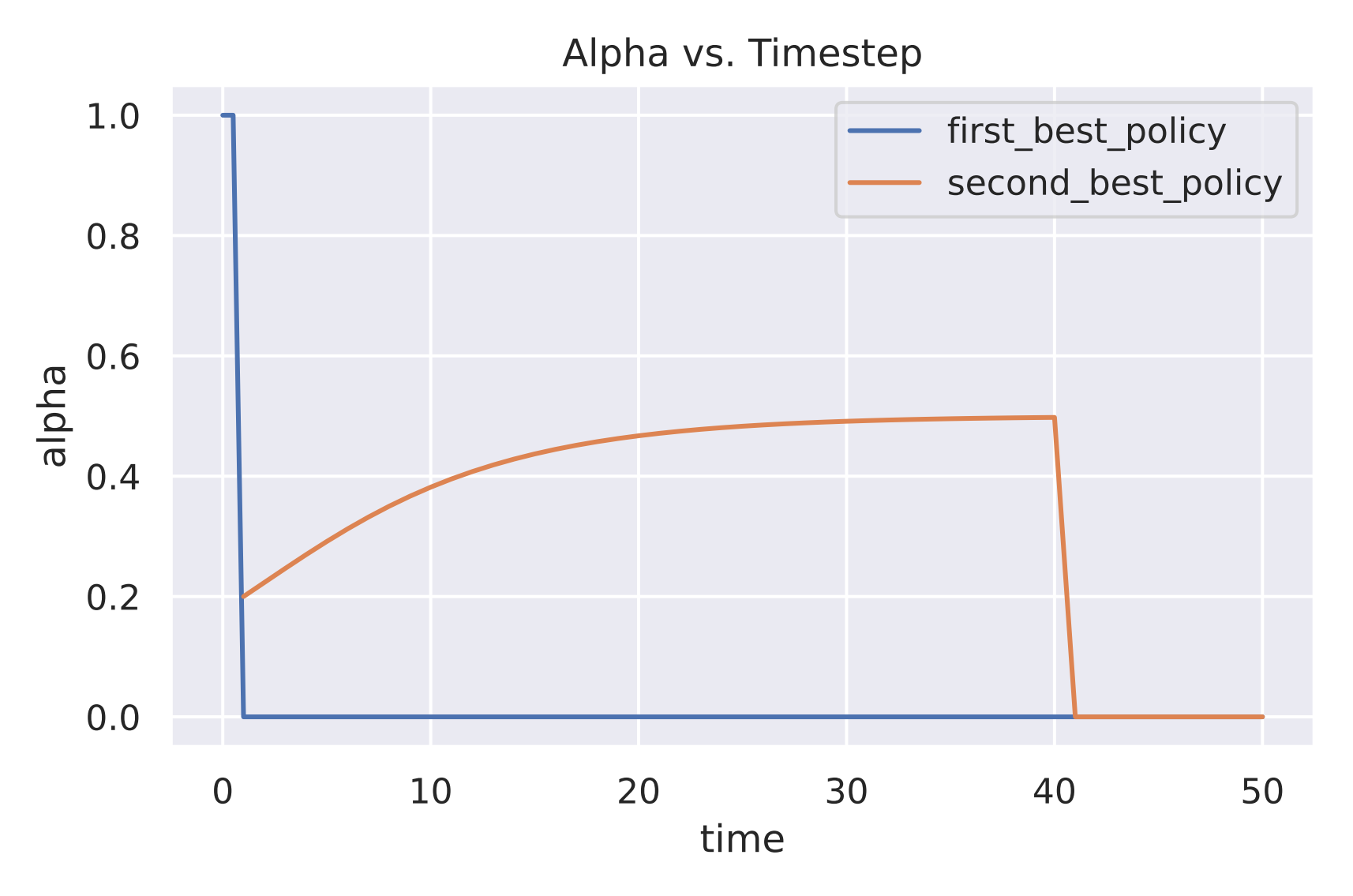
In the second experiment, we compare how α changes within our recommender system problem setting. Here, we initialized {p0, ρ, c, n} = {1/2,1/4,2/3, 1000}. In figure 2, we plot how αt versus t across both polices. We observe that our first best policy spams to all agents and then immediately stops recommending the product. This is because our first best policy violates equation (7) where the agents lose the trust of the policy due to over recommendation of the unknown product. However, we observe a different case in our second best policy where the model only recommends the product to a fraction of the agents. Gradually, this fraction increases until the model loses confidence in the unknown product and stop recommending it. In this case, equation 7 is satisfied for all t and as a result, the policy does not lose the trust of the consumers.